The Basket Of Apples Problem With Tree

Mar 1st, 2019 - written by Kimserey with .

Working with trees is an interesting task. Today we will look into the Basket of Apples problem, which can be solved using a tree structure. This deep dive will allow us to explore how we can reason around trees and understand concepts allowing us to vocalize ideas.

• Basket of Apples
• Implicit Slots
• Point of View
• Formulas

Basket of Apples

Consider the following Basket of Apples problem:

We have four apple baskets with exactly ten apple-slots per basket. With an iterative basket filling process, we start by placing apples in basket A, then once basket A is full, we move to basket B, then basket C, and so on until we either no longer have any apples, or the slots have all been filled, or we reached the limit of slots available.

In this example, limits of slots available are imposed on the amount of apples present between basket A and basket B, and between basket C and basket D. This link is also referred as limit node.

And lastly we want to be able to impose a limit on top of the limit nodes, which would act as a parent limit node for all child baskets.

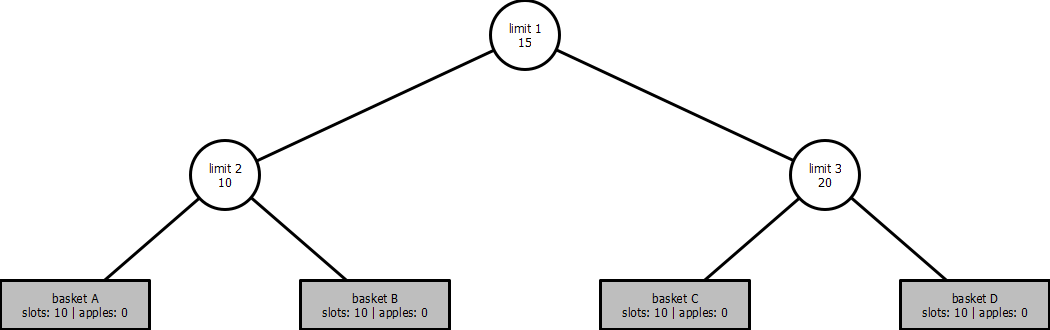
In this example, we have basket A and basket B linked with limit 2, and we have basket C and basket D linked with limit 3. Limit 2 and limit 3 are themselves linked via limit 1. Those limits introduce the following rules:

• Only 10 apples can be placed between basket A and basket B (due to limit 2),
• and 20 apples can be placed between basket C and basket D (due to limit 3),
• but overall only 15 apples can be placed between all baskets (due to limit 1).

Implicit Slots

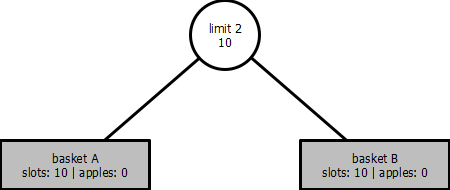
While each baskets have a dedicated slot amount, the limit linking baskets introduces an implicit slot amount. For example, on the subtree between basket A, basket B, and limit 2:

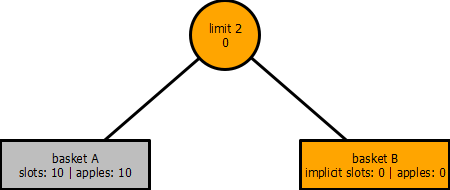
If ten apples are placed in basket A, the implicit slot on basket A and implicit limit imposed by limit 2, from the point of view of basket B, is zero.

Due to limit 2, we are no longer able to accept apples in basket B as basket A used up to the limitation specified. In other word, basket B has ten slots but has an implict slot value of zero.

Point of View

In the previous example, we have seen that basket B has an implicit slot value of zero, and conversely, limit 2 has an implicit limit of zero from the point of view of basket B.

Point of view refers to the standpoint taken to calculate the implicit values of the graph. For example, in the previous subtree, the orange nodes were from the standpoint of basket B.

From basket B standpoint, limit 2 was zero as all the apples were in basket A. But if we take the standpoint of basket A, then basket A slots is ten and limit 2 implicit slots is ten.

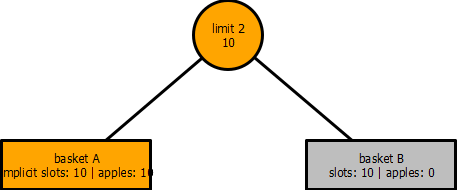
This example demonstrates the existence of multiple perspectives for this particular graph. Each basket has its own perception of the graph, and depending on which basket standpoint we are looking at, the computation of the implicit limits will be different.

Taking a lesser trivial example, we place 5 apples in basket A.

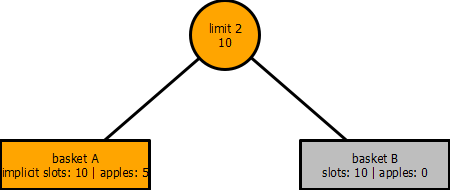
From the point of view of basket A, the implicit slots and limit remain ten.

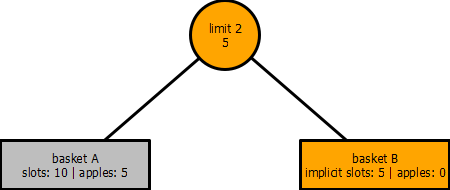
But from the point of view of basket B, the implicit slots have decreased to five due to the implicit limit which decreased to five as well.

Taking the concept of implicit slots and point of view, we can apply it to the whole graph, considering the initial with then apples in basket A, the implicit limit on basket C would be five:

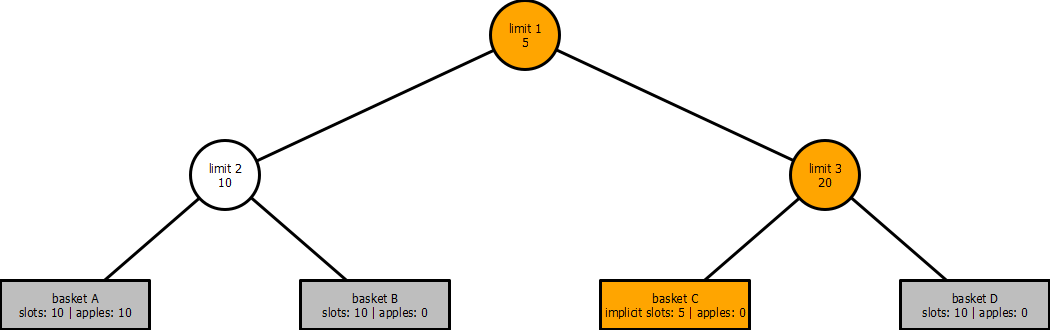
The ten apples placed in basket A have reduced the top parent limit 1 from fifteen to five, resulting in the implicit basket C slots being reduced to five (limit 3 is bypassed as limit 1 < limit 3).

Formulas

The computation of a limit can be expressed from the point of view of a basket:

\[limit\_n_{basket\,x}=limit\_n-\sum{\mathbb{N}\,\backslash\,\{apples_{basket\,x}\}}\quad\text{where}\enspace\mathbb{N}=\{apples_{basket\,A}, apples_{basket\,B}, apples_{basket\,C}, ...\}\text{, from child of}\,limit.\]

The implicit limit of a particular $limit$ from the point of view of $basket\,x$ is computed by taking its $limit$ and substracting the sum of its children baskets amount of $apples$.

For limit 1, from the point of view of basket C, the equation becomes:

\[\begin{split} limit\_1_{basket\,C} &= limit\_1-(apples_{basket\,A}+apples_{basket\,B}+apples_{basket\,D}) \\ limit\_1_{basket\,C} &= 15 - (10 + 0 + 0) \\ limit\_1_{basket\,C} &= 5 \end{split}\]

From the point of view of basket C, the limit imposed by limit 1 is five.

Lastly the computation of the implicit slots on a basket can be represented as:

\[implicit\_slots_{basket\,x}=min\{slots_{basket\,x}, min\enspace \mathbb{P}_{basket\,x}\}\quad\text{where}\enspace\mathbb{P_{basket\,x}}=\text{implicit limits of parents from the point of view of} \enspace basket\,x.\]

Continuing on the point of view of basket C, we can substitute the variables:

\[\begin{split} implicit\_slots_{basket\,C}&=min\{slots_{basket\,C}, min\{limit\_1_{basket\,C},\enspace limit\_3_{basket\,C}\}\} \\ implicit\_slots_{basket\,C}&=min\{10, min\{5, 20\}\}\\ implicit\_slots_{basket\,C}&=5 \end{split}\]

If from here, we place five more apples in basket C, by following those two formulas, we can quickly compute the implicit slots and limits from the point of view of basket D:

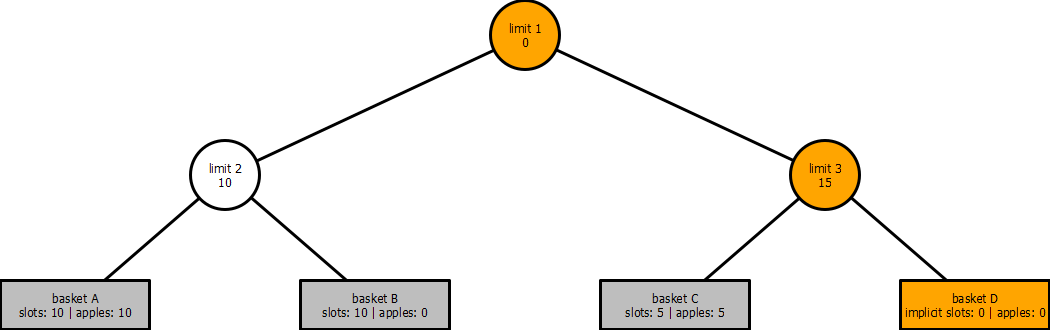
We can compute, from the point of view of basket D, limit 1, limit 3, and the implicit slots of basket D:

\[\begin{split} limit\_1_{basket\,D}&=limit\_1-(apples_{basket\,A}+apples_{basket\,B}+apples_{basket\,C})\\ limit\_1_{basket\,D}&=15 - (10 + 0 + 5)\\ limit\_1_{basket\,D}&=0 \\ \\ limit\_3_{basket\,D}&=limit\_3-(apples_{basket\,C})\\ limit\_3_{basket\,D}&=20-5\\ limit\_3_{basket\,D}&=15\\ \\ implicit\_slots_{basket\,D}&=min\{slots_{basket\,D}, min\{limit\_1_{basket\,D},\enspace limit\_3_{basket\,D}\}\}\\ implicit\_slots_{basket\,D}&=min\{10, min\{0,\enspace 15\}\}\\ implicit\_slots_{basket\,D}&=min\{0, 10, 15\}\}\\ implicit\_slots_{basket\,D}&=0\\ \end{split}\]

And we can see that the result of the computation is five as we expected.

Conclusion

Today we saw how we could solve through mathematical equations the Basket of Apples problem. We started by exploring different scenarios of the problem which we used as basis to test our logic. We then moved on to define the concept of implicit value and point of view which were necessary to discuss about the solution. Lastly we completed the post by extraction mathematical equations from the scenarios which if followed, yield the expect result. I hope you liked this post and I’ll see you on the next one!